Question

Describe a similarity transformation that maps triangle ABC to triangle RST

Answer 1

Given the coordinates of the points A, B, and C:

`\begin{gathered} A=(6,4) \\ B=(-2,0) \\ C=(-4,2) \end{gathered}`

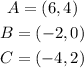
And now, the coordinates of R, S, and T:

`\begin{gathered} R=(2,3) \\ S=(0,-1) \\ T=(1,-2) \end{gathered}`

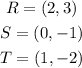
The triangles are:

As we can see, the dilation factor can be determined using the sides of the triangles. The sides BC and ST are similar, and ST is half the length of BC. The same is true for RT ~ AC and RS ~ AB. Then, the dilation factor k is:

`k=(1)/(2)`

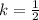
Now, looking at BC and ST are reflected from quadrant II to quadrant IV. Then, we conclude that the reflection is about the line:

`y=x`