Question

segment CD has endpoints at C(0, 3) and D(0, 7). If the segment is dilated by a factor of 3 about point C, what is the length of the image of segment CD question markGroup of answer choices1621412

Answer 1

Step-by-step explanation

We are given the following coordinates of a line segment:

`\begin{gathered} C(0,3) \\ D(0,7) \end{gathered}`

We are required to determine the length of the image of the segment CD after being dilated by a factor of 3.

First, we determine the new coordinates of CD after the dilation as:

`\begin{gathered} C(x,y)\to C^(\prime)(3x,3y) \\ C(0,3)\to C^(\prime)(3*0,3*3)=(0,9) \\ \\ D(x,y)\to D^(\prime)(3x,3y) \\ D(0,7)\to D^(\prime)(3*0,3*7)=(0,21) \end{gathered}`

Therefore, the new coordinates of C and D are C(0, 9) and D(0, 21).

Now, we determine the length of the two points as follows:

`\begin{gathered} C(0,9)\to(x_1,y_1) \\ D(0,21)\to(x_2,y_2) \\ d=√((x_2-x_1)^2+(y_2-y_1)^2) \\ CD=√((0-0)^2+(21-9)^2) \\ CD=√((0)^2+(12)^2) \\ CD=√(0+144)=√(144) \\ CD=12 \end{gathered}`

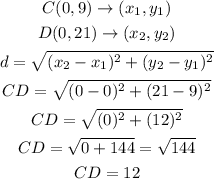
Hence, the length of the image of the segment CD is 12 units.