Question

Donovan wants to earn a 70% in Mr. Mottola's class. He knowshe currently has an 66% in the class after 8 grades. What is theminimum grade Donovan would need to earn in order to have a70%.Help ?

Answer 1

For this case we need to remember the definition of average given by:

`\text{Mean}=(\sum ^n_(i=1)x_i)/(n)`

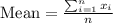
We know that the passing score for the two semestrers is 70%. We also know that the score for Semester 1 is 55

And for semester 2 we have that RC3= 64 and RC4= 78. The average of both RC is:

`Rc=(64+78)/(2)=71`

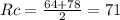
This average represent the 90% of the grade for the second semester. We also know that the final spring exam (SF) is 10% of the second semester grade.

In order to pass we need to satisfy the following:

`(55+\left\lbrack 0.9\cdot(71)+0.1\cdot SF\rbrack\right\rbrack )/(2)=70`

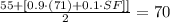
And for this case we want to solve for SF the spring final score required in order to pass. Solving we got:

`SF=((70\cdot2)-55-63.9)/(0.1)=211`

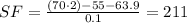
He needs 211 in the final spring exam in order to get an 85 for the second semester and reach the 70% to pass