Question

Find the two positive consecutive odd integers whose product is 63.

Answer 1

GIVEN:

We are given that there are two positive consecutive odd integers whose product is 63.

Required;

To determine these two integers.

Step-by-step solution;

We shall assign variables to the integers for a start. Let the first of the two integers be represented by letter x.

If there are two consecutive odd integers, that means x is an odd number and, the next consecutive odd number would be x + 2.

Note that the number that follows an odd number is ane even number, and this is now followed by the next consecutive odd number. Hence;

`\begin{gathered} First\text{ }odd\text{ }number=x \\ \\ Next\text{ }odd\text{ }number=x+2 \end{gathered}`

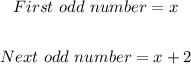
The product of both numbers is 63, therefore we can set up the following equation;

`\begin{gathered} x(x+2)=63 \\ \\ x^2+2x=63 \\ \\ Subtract\text{ }63\text{ }from\text{ }both\text{ }sides: \\ \\ x^2+2x-63=0 \end{gathered}`

Now we can solve the quadratic equation that has resulted from this;

`\begin{gathered} x^2+2x-63=0 \\ \\ Factors\text{ }of\text{ }-63=+9*(-7) \\ \\ Therefore: \\ \\ x^2+9x-7x-63=0 \\ \\ (x^2+9x)-(7x+63)=0 \\ \\ x(x+9)-7(x+9)=0 \\ \\ (x+9)(x-7)=0 \\ \\ x+9=0,x=-9 \\ \\ x-7=0,x=7 \end{gathered}`

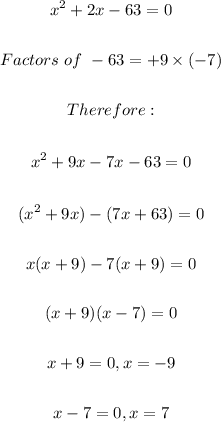
Note that the two numbers are POSITIVE consecutive integers. That means we shall only take the positive value of x.

If the product of both numbers is 63, then where x = 7,

`\begin{gathered} x=7 \\ \\ x+2=(63)/(7) \\ \\ 7+2=(63)/(7) \\ 9=9 \\ \end{gathered}`

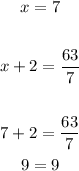
Therefore, the numbers are;

`7\text{ }and\text{ }9`

ANSWER:

The last option is the correct answer