Question

Diana is driving 182 miles to Orlando for a math convention. She has already driven x miles of the trip. If Diana drives below 70 miles per hour for the remainder of the trip, which inequality best represents the amount of time in hours, t, that it will take her to complete the remainder of her drive to Orlando? 182 - A. < 70 B. 1> 182x 70 C.1 182 - 1 182- r 70

Answer 1

The best inequality to represent the time t Diana needs to complete her trip to Orlando, given she has already traveled x miles, is t > (182 - x) / 70. This inequality assumes she will continue to travel at a speed less than 70 miles per hour.

Step-by-step explanation:

The question asks which inequality best represents the amount of time, t, it will take Diana to complete the remainder of her drive to Orlando if she has already driven x miles and has 182 miles in total to drive. If Diana drives at a speed below 70 miles per hour for the remaining distance, we look for an inequality that represents the time taken to travel the remaining distance.

To calculate the remaining distance we subtract the portion already covered, x, from the total distance. This gives us 182 - x miles left to travel. Since Diana drives below 70 miles per hour, the time t to cover the remaining distance at that speed would be greater than the distance divided by the speed.

The suitable inequality that represents this scenario would be:

t > (182 - x) / 70

Answer 2

Given: Diana is driving 182 miles to Orlando for a math convention.

She has already driven x miles of the trip.

So, the remianing distance = (182 - x) miles

Diana drives below 70 miles per hour for the remainder of the trip.

As we know, speed = distance/time

So, the time = distance/speed

The relation between time and speed are inversely

so, when speed decrease, time increase

so, the time of the remaining distance will be:

`t>(182-x)/(70)`

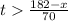
So, the answer is option D