Question

I know you’re supposed to change the bounds and break up the integral, but for some reason, I can’t get the 44/3. Can someone explain how to solve this definite integral?

Answer 1

First, look for the zeroes of the integrand in the interval [0, 6] :

x² - 6x + 8 = (x - 4) (x - 2) = 0 ⇒ x = 2 and x = 4

Next, split up [0, 6] into sub-intervals starting at the zeroes we found. Then check the sign of x² - 6x + 8 for some test points in each sub-interval.

• For x in (0, 2), take x = 1. Then

x² - 6x + 8 = 1² - 6•1 + 8 = 3 > 0

so x² - 6x + 8 > 0 over this sub-interval.

• For x in (2, 4), take x = 3. Then

x² - 6x + 8 = 3² - 6•3 + 8 = -1 < 0

so x² - 6x + 8 < 0 over this sub-interval.

• For x in (4, 6), take x = 5. Then

x² - 6x + 8 = 5² - 6•5 + 8 = 3 > 0

so x² - 6x + 8 > 0 over this sub-interval.

Next, recall the definition of absolute value:

`|x| = \begin{cases}x & \text{for }x \ge0 \\ -x & \text{for }x < 0\end{cases}`

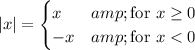
Then from our previous analysis, this definition tells us that

`|x^2 - 6x + 8| = \begin{cases}x^2 - 6x + 8 & \text{for }0<x<2 \text{ or } 4<x<6 \\ - (x^2-6x+8) & \text{for }2<x<4\end{cases}`

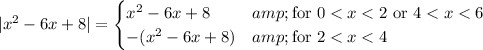
So, in the integral, we have

`\displaystyle \int_0^6 |x^2-6x+8| \, dx = \left\{\int_0^2 - \int_2^4 + \int_4^6\right\} (x^2 - 6x + 8) \, dx`

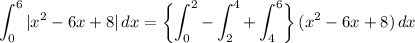
Then

`\displaystyle \int_0^2 (x^2 - 6x + 8) \, dx = \left(\frac13 x^3 - 3x^2 + 8x\right) \bigg|_0^2 = \frac{20}3 - 0 = \frac{20}3`

`\displaystyle \int_2^4 (x^2 - 6x + 8) \, dx = \left(\frac13 x^3 - 3x^2 + 8x\right) \bigg|_2^4 = \frac{16}3 - \frac{20}3 = -\frac43`

`\displaystyle \int_4^6 (x^2 - 6x + 8) \, dx = \left(\frac13 x^3 - 3x^2 + 8x\right) \bigg|_4^6 = 12 - \frac{16}3 = \frac{20}3`

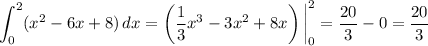
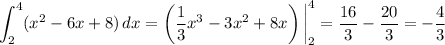
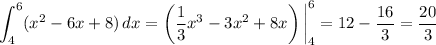
and the overall integral would be

20/3 - (-4/3) + 20/3 = 44/3