Answer:
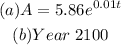
Explanation:
The exponential growth model is given as:

The population in Year 2000 (t=0) = 5.86 million.
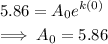
The projected population in Year 2015 (t=15) = 7 million.

We solve the equation for k.
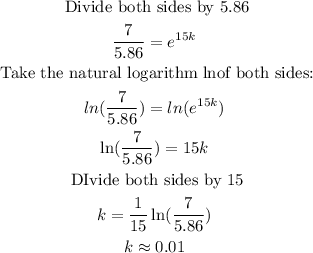
(a)The exponential growth function that models the data is:
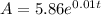
(b)When the population is 16 million, i.e. A=16, we want to find the value of t.
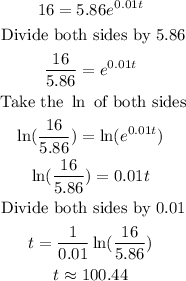
Add 100 to the year 2000:
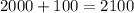
The population will be 16 million in the year 2100.