Question

Find the inflection points of f(x) = 4x^4 + 55x^3 - 21x^2 + 13. (Give your answered as a commas as a separated list) inflection points =

Answer 1

Okay, here we have this:

Considering the provided function, we are going to calculate the inflection points, so we obtain the following:

Let's remember that the inflection points are those where the derivative is equal to zero or is undefined and changes sign, so let's calculate it:

`\begin{gathered} f(x)=4x^4+55x^3-21x^2+13 \\ f^(\prime)^(\prime)(x)=(d^2(4x^4+55x^3-21x^2+13))/(dx^2) \\ f^(\prime)^(\prime)(x)=48x^2+330x-42 \end{gathered}`

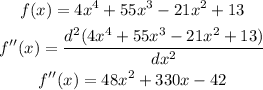
Now let's find the points where the second derivative is zero or undefined:

`\begin{gathered} 48x^2+330x-42=0 \\ x_(1,2)=(-330\pm√(330^2-4\cdot48(-42)))/(2\cdot48) \\ x_(1,2)=(-330\pm342)/(96) \\ x_1=(-330+342)/(96),x_2=(-330-342)/(96) \\ x_1=(12)/(96),x_2=(-672)/(96) \\ x_1=(1)/(8),x_2=-7 \end{gathered}`

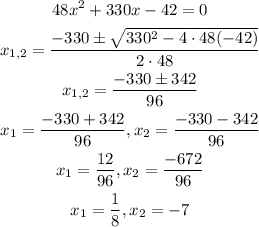
Now we will calculate the third derivative of the function and we will evaluate in these roots, if the result is different from zero then we have an inflection point:

`\begin{gathered} f^(\prime)^(\prime)^(\prime)(x)=(d(f^(\prime)^(\prime)(x)))/(dx) \\ =(d(48x^2+330x-42))/(dx) \\ =96x+330 \end{gathered}`

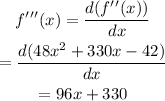
And evaluating in the two roots:

`\begin{gathered} f^(\prime)^(\prime)^(\prime)((1)/(8))=96((1)/(8))+330 \\ =12+330 \\ =342 \\ f^(\prime)^(\prime)^(\prime)(-7)=96(-7)+330 \\ =-672+330 \\ =-342 \end{gathered}`

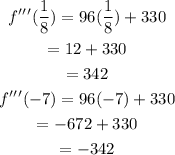
We observe that since the result is different from zero, then the two are inflection points, we substitute in the original function to find the y-coordinate of the points:

`\begin{gathered} f((1)/(8))=4((1)/(8))^4+55((1)/(8))^3-21((1)/(8))^2+13 \\ =(13087)/(1024) \\ f(-7)=4(-7)^4+55(-7)^3-21(-7)^2+13 \\ =-10277 \end{gathered}`

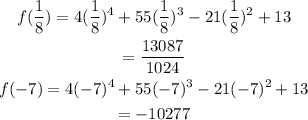
Finally we obtain that the inflection points are: (1/8, 13087/1024) and (-7, -10277).