Given:
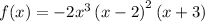
Required:
We need to find the zeros of the function, the end behavior, and the maximum number of turning points and draw the graph.
Step-by-step explanation:
a)
Set f(x)=0 to find the zeros of the given function.

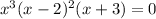

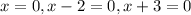
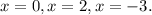
The zeros are 0,2 and -3.
Recall that The number of times a given factor appears in the factored form of the equation of a polynomial is called the multiplicity.
The multiplicity 0 is 3.
The multiplicity 2 is 2.
The multiplicity -3 is 1.
b)
The end behavior:
Taking the limit of negative infinity to the given function.
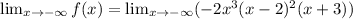
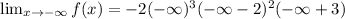
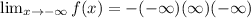
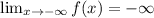

Taking the limit of infinity to the given function.
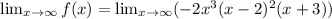
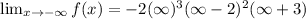
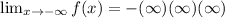
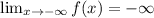
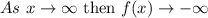
Recall that the maximum number of turning points of a polynomial function is always one less than the degree of the function.
The degree of the given function is 3+2+1=6.
The maximum number of turning points =6-1=5.
Final answer:
a)
Zeros of the function
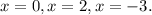
The multiplicity 0 is 3.
The multiplicity 2 is 2.
The multiplicity -3 is 1.
b)
End behavior:

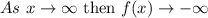
The maximum number of turning points is 5.
c)
The graph of the given function