Answer:
Approximately
 .
.
Step-by-step explanation:
Let
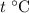 be the final temperature of the water and the iron.
be the final temperature of the water and the iron.
Temperature of the water would be increase by
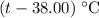 .
.
Temperature of the iron would be reduced by
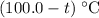 .
.
Let
 denote the specific heat of each material. Let
denote the specific heat of each material. Let
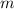 denote the mass of the material. For a temperature change of
denote the mass of the material. For a temperature change of
 , the energy change involved would be:
, the energy change involved would be:
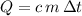 .
.
The energy that the water need to absorb would be:
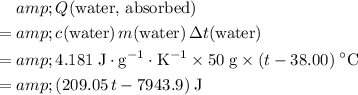 .
.
The energy that the iron would need to release would be:
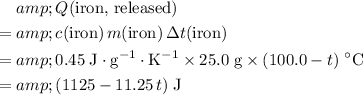 .
.
Since this calorimeter is insulated, the energy that the iron had released would be equal to the energy that the water had absorbed:
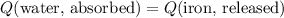 .
.
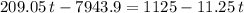 .
.
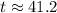 .
.
Thus, the final temperature of the water and the iron would be approximately
 .
.