Question

Reflect AABC over the x-axis, then translate left 4 units

Answer 1

To reflect triangle ABC over the x-axis simply means the image will form a mirror image of each other over the x axis. Reflection over the x axis simply implies we negate the value of y-coordinate but live the x-coordinate the same . Therefore reflecting this

`\begin{gathered} A(1,1) \\ B(1,5) \\ C(5,2) \end{gathered}`

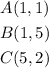
over x -axis will be

`\begin{gathered} A^(\prime)(1,-1) \\ B^(\prime)(1,-5) \\ C^(\prime)(5,-2) \end{gathered}`

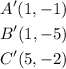
Then translating left 4 units will be

`\begin{gathered} A^(\prime)(-3,-1) \\ B^(\prime)(-3,-5) \\ C^(\prime)(1,-2) \end{gathered}`

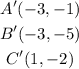
The new point on the graph will be