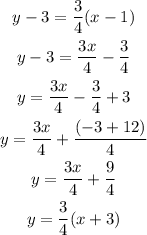Question

Write an equation in point-slope form of the line that passes through the given points(1,3) and (-3,0) or with the given characteristics

Answer 1

`y=(3)/(4)(x+3)`

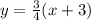
Step-by-step explanation:

The point-slope form of the equation of a line is generally given as;

`y-y_1=m(x_{}-x_1)_{}`

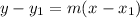
where m = slope of the line

x1 and y1 = coordinates of the point.

Let's 1st of all determine the slope of the line that passes through the points with coordinates x1 = 1, x2 = -3, y1 = 3, and y2 = 0 using the below formula;

`m=(y_2-y_1)/(x_2-x_1)=(0-3)/(-3-1)=(-3)/(-4)=(3)/(4)`

Let's go ahead and write the equation of the line in point-slope form using m = 3/4 and x1 = 1 and y1 = 3;

`\begin{gathered} y-3=(3)/(4)(x-1) \\ y-3=(3x)/(4)-(3)/(4) \\ y=(3x)/(4)-(3)/(4)+3 \\ y=(3x)/(4)+((-3+12))/(4) \\ y=(3x)/(4)+(9)/(4) \\ y=(3)/(4)(x+3) \end{gathered}`