Question

What is an equation of the line that passes through the point (-2, -3) and isperpendicular to the line x + 3y = 24?

Answer 1

In this case, we'll have to carry out several steps to find the solution.

Step 01:

Data

point (-2,-3) x1 = -2 y1 = -3

x + 3y = 24

Step 02:

m' = - 1 / m ---> slope of the perpendicular line

3y = - x + 24

y = (- x + 24) / 3

`y\text{ = }\frac{-x}{3\text{ }}+(24)/(3)\text{ = }(-1)/(3)x\text{ +8}`
`m\text{'}=\text{ (}(-1)/(-(1)/(3)))\text{ = 3}`

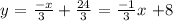
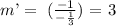
Point-slope form of the line

(y - y1) = m (x - x1)

( y - (-3)) = 3 (x - (-2))

y +3 = 3 (x + 2)

y = 3x + 6 -3

y = 3x +3

The solution is:

The perpendicular line equation is:

y = 3x +3