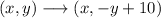Question

x For Exercises 25-28, what is a reflection rule that maps each triangle and its image? 26. G(9, 12), H(-2. - 15), (3, 8) and G (9,-2), H(-2,25), (3, 2)

Answer 1

The points we have for the triangle are:

G(9, 12), H(-2, - 15), J(3, 8)

G'(9,-2), H'(-2, 25), J'(3, 2)

The points marked with " ' "are the image points.

In a coordinate pair, the first number is always the x-coordinate, and the second number is the y-coordinate: (x,y)

In this case, analyzing the points, from G, to the image G' the x-coordinate , which is 9, stays the same.

If we look at the points H and H' we can see that the x-coordinate, which is -2, stays the same.

And for points J and J', the x-coordinate which is 3, stays the same.

Now, for the y-coordinates, if we analyze the points G(9,12) and G'(9,-2). We can see that y-coordinate went from 12 to -2. This change is represented by:

-y+10

Because the original y which is 12, if we multiply it by -, we get -12, and if we add 10 to that we get -12+10=-2.

We can confirm this for the other points, the y-coordinate of H is -15, if we transform it as -y+10:

`\begin{gathered} -y+10 \\ -(-15)+10 \\ 15+10=25 \end{gathered}`

We get the y-coordinate for H' which is 25.

That is also true for the third point J and J'.

In summary, the reflection rule that maps this triangle to its image is:

`(x,y)\longrightarrow(x,-y+10)`