Given,
Mass of the block, m=2.0 kg
The initial speed of the block, u=5.0 m/s
The distance traveled by the block, d=0.80 m/s
As the block comes to rest at the end of the motion, the final velocity of the block, v=0 m/s
From the equation of the motion,
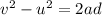
Where a is the acceleration of the block.
Rearranging the above equation,
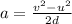
On substituting the known values,
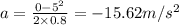
The frictional force acting on it can be calculated as
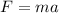
Substituting the known values,
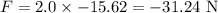
The energy lost due to friction can be calculated as,
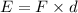
Therefore the energy lost due to friction is,
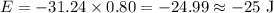
The negative sign indicates th