Question

Solve the system by graphing7x + 3y = -12x – 3y=-12

Answer 1

Here, we want to solve the system of equation by graphing

To do this, we plot the graph of both lines on the same graph; the point at which the lines meet is the solution to the sysyem of equations

For ease of plotting, we need two points that we can join for each line

The x-intercept and the y-intercept

Generally, the equation of a straight line is;

`y\text{ = mx + c}`

where m is the slope and c is the y-intercept

To get the x-intercept, simpy set y to 0; to get the y -intercept, simply set x to zero

For; 7x + 3y = -12

For x-intercept;

`\begin{gathered} 7x\text{ + 3(0) = -12} \\ \\ 7x\text{ = -12} \\ \\ x\text{ = }(-12)/(7) \\ \\ For\text{ y-intercept} \\ \\ 7(0)\text{ + 3y = -12} \\ \\ 3y\text{ = -12} \\ y\text{ = }(-12)/(3) \\ \\ y\text{ = -4} \end{gathered}`

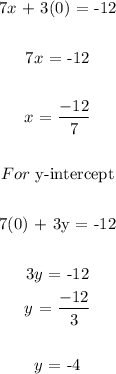
To plot the graph of the line, simply join the points (-12/7,0) and (0,-4) with a straight line

For x - 3y = 12

`\begin{gathered} To\text{ get x-intercept} \\ \\ \text{set y = 0} \\ \\ \text{here x = 12} \\ \\ To\text{ get y-intercept, set x = 0} \\ \\ -3y\text{ = -12} \\ \\ y\text{ = }(-12)/(-3) \\ \\ y\text{ = 4} \end{gathered}`

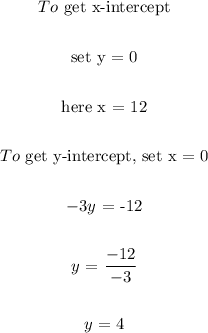
So to plot the graph of this, simply join the points (12,0) and (0,4) with a line

The point at which the line of both intersects is the solution to the system of equation