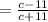Given:
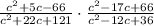
You need to follow these steps in order to multiply the Rational Expressions and express the product in the simplest form:
1. Factor the numerator of the expression on the left by finding two numbers whose sum is 5 and whose product is -66, as follows:
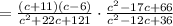
2. Factor the numerator of the second expression by finding two numbers whose sum is -17 and whose product is 66:
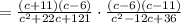
3. Factor the denominator of the expression on the left by finding two numbers whose sum is 22 and whose product is 121.
4. Factor the denominator of the expression on the right by finding two numbers whose sum is -12 and whose product is 36.
Then, you get:
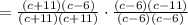
5. You know that:
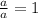
Then, you can simplify:
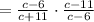
6. Multiply the numerators and multiply the denominators:
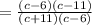
7. Simplifying, you get:
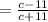
Hence, the answer is: