Question

Match the expression on the left with the correct simplified expression on the right.

Answer 1

Given: The expression below

`\begin{gathered} (((3x^3y^4)^3)/((3x^2y^2)^2))^2 \\ (((3x^4y^2)^4)/((3x^5y^2)^3))^2 \end{gathered}`

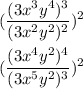
To Determine: The matching expression to the given expressions

Solution

Let us simplify each of the expressions using exponents rule

`\begin{gathered} Exponent-Rule1=(a^m)^n=a^(m* n) \\ Exponent-Rule2=((a^m)/(a^n))=a^(m-n) \end{gathered}`

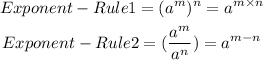
Applying the exponent rule 1 above to the given expressions

`\begin{gathered} (3x^3y^4)^3=3^3x^(3*3)y^(4*3)=27x^9y^(12) \\ (3x^2y^2)^2=3^2x^(2*2)y^(2*2)=9x^4y^4 \end{gathered}`
`\begin{gathered} (3x^4y^2)^4=3^4x^(4*4)y^(2*4)=81x^(16)y^8 \\ (3x^5y^2)^3=3^3x^(5*3)y^(2*3)=27x^(15)y^6 \end{gathered}`

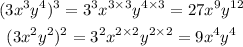
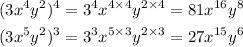
Applying the exponent rule 2

`((3x^(3)y^(4))^(3))/((3x^(2)y^(2))^(2))=(27x^9y^(12))/(9x^4y^4)=(27)/(9)x^(9-4)y^(12-4)=3x^5y^8`
`((3x^(4)y^(2))^(4))/((3x^(5)y^(2))^(3))=(81x^(16)y^8)/(27x^(15)y^6)=(81)/(27)x^(16-15)y^(8-6)=3xy^2`

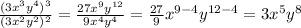
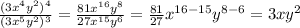
Let us not apply exponent rule 1 above

`(((3x^(3)y^(4))^(3))/((3x^(2)y^(2))^(2)))^2=(3x^5y^8)^2=3^2x^(5*2)y^(8*2)=9x^(10)y^(16)`
`(((3x^(4)y^(2))^(4))/((3x^(5)y^(2))^(3)))^2=(3xy^2)^2=3^2x^2y^(2*2)=9x^2y^4`

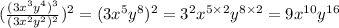
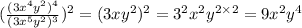
Hence, the matching is as shown below