The question says that the odds against Deborah winning first prize in the chess tournament are 2 to 11. These are the odds of her not winning.
Odds of an event is related to the probability of the same event occuring by the formula:
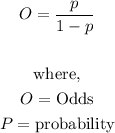
Therefore, to calculate the probability of the event occurring, we simply make p the subject of the formula:

Now that we have the formula for probability (p) in terms of odds (O), we can proceed to find the probability of Deborah NOT winning first prize. This is done below:

The question asks us to find the probability that Deborah wins the first prize. This is the direct opposite event or the mutually exclusive event to her NOT winning.
The relationship between event (P) and its opposite, event (Q) is:
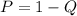
Therefore, to find the probability (Q) of Deborah winning first prize is:

Therefore the probability of Deborah winning the first prize is: 11/13