Question

Suppose we want to choose 2 objects, without replacement, from the 5 objects pencil, eraser, desk, chair, and lamp.(a)How many ways can this be done, if the order of the choices is taken into consideration? (b)How many ways can this be done, if the order of the choices is not taken into consideration?

Answer 1

Step-by-step explanation

This question is actually a problem of permutations and combinations. In option (a) we must the number of possible ways to arrange 2 items from a total of 5 taken order into account. This means that we must give the number of permutations for selecting 2 items out of 5. The number of permutations for selecting k items out of a total of n is given by the following formula:

`P=(n!)/((n-k)!)`

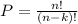
Here we have n=5 and k=2 so we get:

`P=(5!)/((5-2)!)=(5!)/(3!)=(120)/(6)=20`

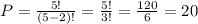
In option (b) the order doesn't matter. In this case we must give the number of combinations. For a selection of k items out of a total of n the formula for the number of combinations is:

`C=(n!)/((n-k)!k!)`

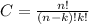
In this case n=5 and k=2 so we get:

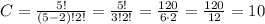
`C=(5!)/((5-2)!2!)=(5!)/(3!2!)=(120)/(6\cdot2)=(120)/(12)=10`Answer

Then the answers are:

(a) 20

(b) 10