Question

7. Here is a graph of the equation 3x - 2y = 12. Select ALL coordinate pairsthat represent a solution to the equation.*(2, -3)(4, 0)(5, -1)(0, -6)(2, 3)

Answer 1

To check if a pair is a solution of an equation, we just need to replace the values for x and y-coordinates in the equation. If the equality is satisfied, then the pair is a solution to the equation.

Let's check each of the pairs given:

(2, -3) has 2 as its x-value and -3 as its y-value. Replacing those in the equation:

`\begin{gathered} 3x-2y=12 \\ 3(2)-2(-3)=12 \\ 6-(-6)=12 \\ 6+6=12 \\ 12=12 \end{gathered}`

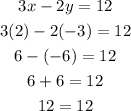
We can see that by solving the equation, we obtain 12 on both sides of the equation. The equality is satisfied, then the pair (2, 3) represents a solution to the equation.

Following the same process for the others:

(4, 0):

`\begin{gathered} 3\cdot4-2\cdot0=12 \\ 12-0=12 \\ 12=12 \end{gathered}`

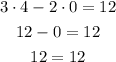
It is a solution.

(5, -1):

`\begin{gathered} 3\cdot5-2\cdot(-1)=12 \\ 15+2=12 \\ 17=12 \end{gathered}`

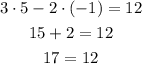
Is NOT a solution.

(0, -6):

`\begin{gathered} 3\cdot0-2\cdot(-6)=12 \\ 0+12=12 \\ 12=12 \end{gathered}`

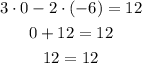
Is a solution.

(2, 3):

`\begin{gathered} 3\cdot2-2\cdot3=12 \\ 6-6=12 \\ 0=12 \end{gathered}`

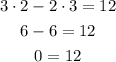
Is NOT a solution.

Now we have checked all. In summary:

(2, -3): Solution

(4, 0): Solution

(5, -1): No solution

(0, -6): Solution

(2, 3): No solution