Question

Hello! Need some help on this question with parts a,b, and c. The rubric is linked below as well. Thank you!

Answer 1

Step-by-step explanation:

Part A.

In part A, we need to identify if offer A can be represented by an arithmetic or geometric series and define the equation for An which is the salary after n years.

Before we start answering, let's review the differences between a geometric sequence and an arithmetic sequence:

• Arithmetic sequence: ,There is a constant difference between each consecutive number. This can be an addition or a subtraction of that common difference.

,

• Geometric sequence: ,Each number is the result of multiplying or dividing the previous number by a common ratio. It is different from the arithmetic sequence because in this case, each consecutive number is the result of a multiplication or division of the previous number.

Justification: In part A, each year the salary increases by 5% which means that each year the salary is multiplicated by 1.05. Since the new salary is the result of multiplying the previous salary, the situation can be represented by a Geometric sequence.

Arithmetic/geometric: Geometric

Equation: The equation is found as follows:

`A_n=a_1r^(n-1)`

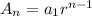
Where An is the amount after n years, and a1 is the initial amount. In this case, since the initial salary is 55,000

`a_1=55,000`

Also, r is the common ratio, as we already mentioned, because there is a 5% increase, the new salary each year is the result of multiplying the previous one by 1.05, that is the common ratio:

`r=1.05`

`\boxed{A_n=55000(1.05)^(n-1)}`

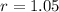
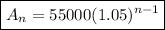
Part B.

In offer B, the starting salary is

`a_1=56000`

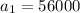
And each year the salary increases by 2,000:

`d=2000`

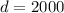
Justification: Since each year there is a constant increase of 2000 in the salary, there will be a constant difference between each consecutive number in the sequence, therefore, the situation for B can be represented by an arithmetic sequence:

Arithmetic/geometric: Arithmetic.

Equation: For an arithmetic sequence the equation is:

`A_n=a_1+(n-1)d`

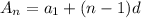
In this case:

`\boxed{A_n=56000+(n-1)(2000)}`

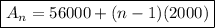
Part C.

Which offer will provide a greater total income after 5 years?

To solve this problem, we use our two equations with n=5.

For A:

`\begin{gathered} A_n=55,000(1.05)^(n-1) \\ \downarrow \\ A_5=55,000(1.05)^(5-1) \\ \downarrow \\ A_5=55,000(1.05)^4 \\ \downarrow \\ A_5=55,000(1.215506) \\ \downarrow \\ \boxed{A_5=66,852.84} \end{gathered}`

For B:

`\begin{gathered} A_n=56,000+(n-1)(2,000) \\ \downarrow \\ A_5=56,000+(5-1)(2,000) \\ \downarrow \\ A_5=56,000+(4)(2,000) \\ \downarrow \\ A_5=56,000+8,000 \\ \downarrow \\ \boxed{A_5=64,000} \end{gathered}`

Justification: The income in 5 years for offer A is above 66,000 and the income in 5 years for offer B is 64,000. Since the result for the offer, B is lower than the result for offer A, the correct offer is A.

The correct offer: A