Question

Answer part B3/2 is not the correct answer believe me I've tried :(

Answer 1

You know that:

- The software is installed onto one computer at a time.

- The software installs at a constant rate.

- She can install on each computer:

`(2)/(3)program`

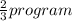
- And she can do it in:

`(1)/(4)hour`

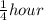
Part A

Let be "x" the time (in hours) it takes to install the whole software program on one computer.

Knowing the information shown before, you can set up the following proportion:

`((1)/(4))/((2)/(3))=(x)/(1)`

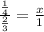
Notice that you can solve for "x" in order to find its value:

`\begin{gathered} ((1)/(4))/((2)/(3))=x \\ \\ x=(3)/(8) \end{gathered}`

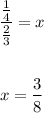
Part B

Let be "t" the time (in hours) it takes to install the software program on 4 computers.

You can identify that it is: