Question

a cone has a radius of 20 mm and a slant height of 38 mm as shown in the diagram . what is the volume of the cone to the nearest cubic meter

Answer 1

0.000013527m^3

Step-by-step explanation:

volume of the cone is expressed as shown;

`V\text{ = }(1)/(3)\pi r^2h`

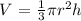
r is the radius = 20mm

h is the height

Given slant height l = 38mm

Using the pythagoras theorem;

l^2 = h^2 + r^2

38^2 = h^2 + 20^2

h^2 = 38^2 - 20^2

h^2 = 1,444 - 400

h^2 = 1044

h = \sqrt[1044]

h = 32.31mm

Get the volume;

Converting to m^3

1mm^3 = 1e-9m^3

13,527mm^3 = x

x = 13,527 * 1e-9

x = 0.000013527m^3

Hence the volume of the cone to nearest cubic meters is 0.000013527m^3