We have the following quadratic function:
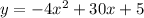
Since a quadratic function represents a parabolla, we have a different meaning for each coefficient. In this case, we have the following:
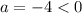
first, we have that the main coefficient is -4, which is less than 0. Thus, the parabola will be wider. In the context of this problem, this means that the ball will take more time to touch the ground.
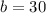
the second coefficient determines, along with the coefficient 'a', to which side the parabolla will move with respect of the y-axis. In this case, since a<0 and b>0, we have that the parabolla will move to the right of the y-axis. Which is clear, since we are measuring with only positive values of the time.
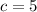
finally, the last coefficient is 5, which represents a constant and the y-intercept of the parabolla. Therefore, in this case it represents the initial height of the ball