4) We have to calculate how many times taller is the actual monument compared to the model.
The actual height is 87 1/2 ft.
The model height is 1 1/4 ft.
We can calculate how many times taller is the actual monument compared to the model by dividing the actual height by the model height:

Answer: the monument is 70 times taller than the model.
The operation we use to solve this problem is a quotient between the two heights.
5) We have a monument that is a rectangular prism.
We know that the height is 5' 2'' and the width is 4' 3''.
We also know that the width (W) is 5 inches less than half the length.
We have to find the length (L).
We then have to write:
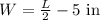
To solve this, we have to add 5 inches to the width first and then multiply the result by 2:
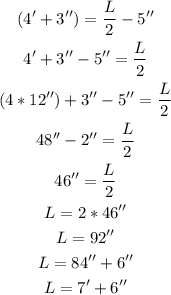
Answer: the length is 7' 6''.
The first operation is adding (we add 5'' to the width) and the second operation is multiplication (we multiply the result by 2).