Question

Please help me solve this in the quickest way possible

Answer 1

Since the polynomial that we want has the roots 3 and i, then the complex conjugate of i is also a root, therefore, the polynomial with roots 3 and i must have another root: -i.

Then, the function will have 3 zeros: 3, i and -i, and it will be of third degree.

The function f(x) in factored form is the following:

`\begin{gathered} f(x)=(x-3)(x+i)(x-i)=(x-3)(x^2+1) \\ \Rightarrow f(x)=(x-3)(x^2+1) \end{gathered}`

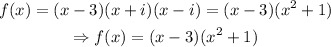
the answer in standard form is:

`f(x)=(x-3)(x^2+1)=x^3-3x^2+x-3`

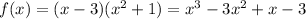
Since the function is a polynomial of third degree, we have the following limits:

`\begin{gathered} \lim _(x\rightarrow\infty)f(x)=\infty \\ \lim _(x\rightarrow-\infty)f(x)=-\infty \end{gathered}`

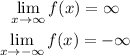
Finally, the y-intercept can be found by making x=0 and solving for y:

`\begin{gathered} y=f(0)=0^3-3(0)^2+0-3 \\ y=-3 \end{gathered}`

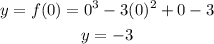
therefore, the y-intercept is x=-3