Question

The following table shows parts of the result of the javelin throw finals at the olympics 2020 (Tokyo).(a) Compute the (arithmetic) mean of the distances. (b) Compute the variance of the distances.

Answer 1

So first we need to find the mean of this set. This value is given by adding all the elements in the set and dividing that result by the total number of elements. In this case it would be the sum of all the distance divided by 8 since there are 8 different distances:

`(87.58+86.67+\cdots+83.30+83.28)/(8)=84.9875`

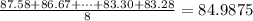
So the mean is 84.9875 and that's the answer to part a.

In part b we must calculate the variance. This value is given by the sum of the square deviations divided by the total number of elements. The square deviations (S) are the squares of the difference between each element and the mean:

`S=(x-\mu)^2`

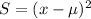
Where S is the square deviation, x the value of the element and the greek letter μ is the mean. In this case x would be each distance and μ=84.9875. So the square deviations are given by:

`S=(x-84.9875)^2`

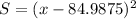
We need to calculate this quantity for each of the 8 distances. Then we add the 8 results and we divide them by 8. This way we find the variance. In the following table you can see the distances, the square deviation of each and the values of the mean and the variance:

Then, the answer to part a is 84.9875 and to part b is 2.1731.