Step 1: Write out the given functions
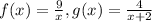
Step 2: Find 1/f and g/f
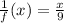
Therefore,
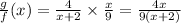
The domain of f is (-∞, ∞) \ {0}.
The domain of g is (-∞, ∞)
If x + 2 = 0, then x = -2.
Therefore g/f is undefined at x = -2.
Hence, the domain of g/f is (-∞, ∞) \ {-2,0}.
Therefore, the domain of g/f is (-∞, -2) ∪ (-2, 0) ∪ (0, ∞)