The given function is
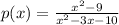
At first, factorize up and down
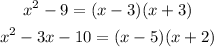
Then the zeroes of the function are -3, 3, and the values of x which make the function undefined are -2, 5
Then p(x) is positive at the values of x

You can see that from the graph of the function
The graph shows that p(x) is positive (over the x-axis at 3 intervals
