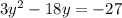
Before we can solve for the value of y, let's convert first the equation into a standard form ax² + bx + c = 0. Let's add 27 on both sides of the equation.
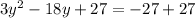
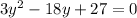
Now, let's solve for the value of y.
Notice that the equation above is factorable by 3. Hence, the equation can also be written as:
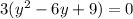
Now, what we have to do is equate the quadratic equation in the parenthesis to zero and solve for y.
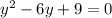
Since the leading term is y² and its numerical coefficient is 1, we can find the factors of this equation by finding the factors of the constant term 9 that add up to the middle term -6.
Factors of 9
a. 3 and 3 → sum is 6
b. -3 and -3 → sum is -6
So, the factor of 9 that add up to -6 is just -3.
Hence, the equation can be factored into:

Equate the factor to zero and solve for y.
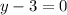
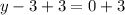
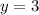
Therefore, the value of y is 3.
Let's check if this is correct.
Replace the variable y in the original equation with 3.

Then, simplify.


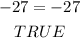
Indeed, by replacing the variable "y" with 3, both sides are equal to -27. Hence, the answer is correct.
ANSWER:
The value of y is 3.