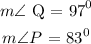Question

Find the measure of each of the indicated angle,side, or diagonal in the parallelograms

Answer 1

To solve the problem, we need to apply the rule

The opposite angles of a parallelogram are equal

The adjacent angles of a parallelogram are supplementary

Hence, we can write:

`12x\text{ -11 = 10x + 7}`

Solving for x:

`\begin{gathered} Collect\text{ like terms} \\ 12x\text{ - 10x = 7 + 11} \\ 2x\text{ = 18} \\ Divide\text{ both sides by 2} \\ (2x)/(2)\text{ =}(18)/(2) \\ x\text{ = 9} \end{gathered}`

Substitute the value of x into the expression for Q

`\begin{gathered} \angle Q\text{ = 12x - 11} \\ =\text{ 12 }*\text{ 9 - 11} \\ =\text{ 97}^0 \end{gathered}`

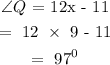
Solving for angle P

`\begin{gathered} \angle Q\text{ + }\angle P\text{ = 180} \\ \angle P\text{ = 180 - }\angle Q \\ \angle P\text{ = 180 - 97} \\ =\text{ 83}^0 \end{gathered}`

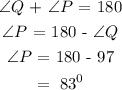
Answer summary

`\begin{gathered} m\angle\text{ Q = 97}^0 \\ m\angle P\text{ = 83}^0 \end{gathered}`