Question

Between 1990 and 1999, the number of movie screens increased by 1500 per year. There were 20690 movie screens in 1990. Use a linear model to (a) determine how many movie screens there were in 1995 and (b) in what year were there 32690 movie screens.-use more than one strategy-use organization skills and verbally explain(ex charts,diagrams, number, table)

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Explain linear models

Linear models are a way of describing a response variable in terms of a linear combination of predictor variables. The response should be a continuous variable and be at least approximately normally distributed. It is given by the following equation.

`\begin{gathered} y=mx+b\text{ } \\ \text{where m is the slope} \end{gathered}`

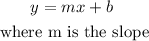
STEP 2: Get the linear model for the statements

`\begin{gathered} constant=20690 \\ i\text{t increases by 1500 per year, year is given as x where x is the number of years after 1990} \\ increment=1500x \\ \\ \therefore\text{The linear model of the scenario is given as:} \\ y=20690+1500x \end{gathered}`

STEP 3: Determine the value of x for year 1995

`\begin{gathered} Starting\text{ year is 1990,} \\ x=0 \\ \text{For 1991,} \\ x=1 \\ \text{For 1992,} \\ x=2 \\ For\text{ 1993,} \\ x=3 \\ \text{For 1994,} \\ x=4 \\ \text{For 1995,} \\ x=5 \end{gathered}`

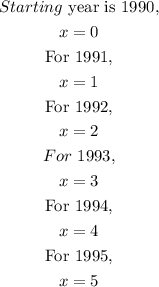
STEP 4: Use the linear model to determine how many movie screens there were in 1995

Using the linear model given in Step 2, the movie screen in 1995 will be:

`\begin{gathered} y=20690+1500x \\ x=5 \\ By\text{ substitution,} \\ y=20690+1500\left(5\right)=20690+7500=28190 \end{gathered}`

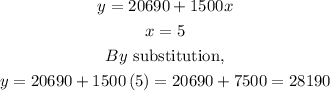
Hence. the number of movie screens in 1995 is 28190

STEP 5: Get the value of x for 32690 movie screens

`\begin{gathered} y=20690+1500\left(x\right) \\ y=32690,x=? \\ by\text{ substituion,} \\ 32690=20690+1500x \\ Subtract\text{ 20690 from both sides} \\ 32690-20690=20690+1500x-20690 \\ 12000=1500x \\ Divide\text{ both sides by 1500} \\ (12,000)/(1500)=(1,500x)/(1500) \\ 8=x \\ x=8 \end{gathered}`

STEP 6: Get the year equivalent to x =8

`\begin{gathered} When\text{ }x=0\text{, year is 1990} \\ When\text{ }x=8\text{, year will be 1990+8=1998} \\ \\ \therefore year=1998 \end{gathered}`

Hence, the year that has 32690 movie is 1998