Question

In the exponential function f(x) = 3^-x + 2, what is the end behavior of f(x) as x goes to ∞?

Answer 1

Step-by-step explanation

So we must find the end behaviour of the following function when x tends to infinite:

`f(x)=3^(-x)+2`

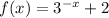
This basically means that we must find the following limit:

`\lim_(x\to\infty)f(x)=\lim_(x\to\infty)(3^(-x)+2)`

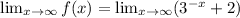
Before continuing it would be a good idea to remember the following property of powers:

`a^(-n)=(1)/(a^n)`

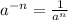
So if we apply this property to f(x) we get:

`f(x)=(1)/(3^x)+2`

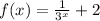
So the limit that we have to calculate is:

`\lim_(x\to\infty)f(x)=\lim_(x\to\infty)((1)/(3^x)+2)`

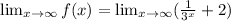
When x tends to infinite the exponential term 3ˣ also tends to infinite. This means that when x tends to infinite the term 1/3ˣ tends to 1 divided by infinite. A constant divided by an expression tending to infinite always tends to 0 since you are dividing a fixed number by another that keeps increasing. Then the limit above is:

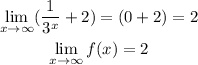
`\begin{gathered} \lim_(x\to\infty)((1)/(3^x)+2)=(0+2)=2 \\ \lim_(x\to\infty)f(x)=2 \end{gathered}`Answer

Then the answer is that f(x) tends to 2 when x tends to infinite.