Question

For a certain company, the cost for producing x items is 45x + 300 and the revenue for selling x item is 85x-0.5x^2. Set up an expression for the profit from producing and selling x items. We assume that the company sells all of the items that it produces. (Hint: it is a quadratic polynomial.)Find two values of x that will create a profit of $300Is it possible for the company to make a profit of $15,000?

Answer 1

In order to find the expression for the profit, let's subtract the revenue and the cost:

`\begin{gathered} Profit=Revenue-Cost\\ \\ Profit=85x-0.5x^2-(45x+300)\\ \\ Profit=-0.5x^2+40x-300 \end{gathered}`

Now, to find two values of x that create a profit of 300, let's use Profit = 300 and solve for x:

`\begin{gathered} 300=-0.5x^2+40x-300\\ \\ -0.5x^2+40x-600=0\\ \\ x^2-80x+1200=0\\ \\ x=(-b\pm√(b^2-4ac))/(2a)\\ \\ x=(80\pm√(6400-4800))/(2)\\ \\ x_1=(80+40)/(2)=(120)/(2)=60\\ \\ x_2=(80-40)/(2)=(40)/(2)=20 \end{gathered}`

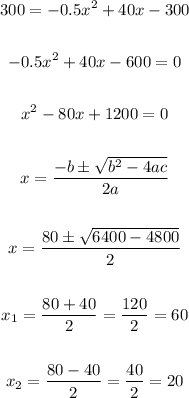
Therefore the two values are x = 20 and x = 60.

Now, let's find if the profit can be $15,000:

`\begin{gathered} 15000=-0.5x^2+40x-300\\ \\ -0.5x^2+40x-15300=0\\ \\ x^2-80x+30600=0\\ \\ x=(-b\pm√(b^2-4ac))/(2a)\\ \\ x=(80\pm√(6400-122400))/(2)\\ \\ x=40\pm(√(-116000))/(2)\\ \\ x=40\pm170.29i \end{gathered}`

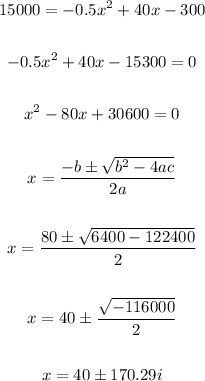
Since the solutions are complex numbers, therefore the answer is NO.