Question

Which ordered pair is a solution of the equation7x-2y= -5

Answer 1

We are given the following equation:

`7x-2y=-5`

Since we have two variables "x" and "y" and only one equation, this means that this system has infinite solutions. In fact, all the ordered pairs that are solutions to this equation are located in a straight line, the equation of the said line can be found by solving for "y" in the equation. Like this:

`7x-2y=-5`

subtracting 7x in both sides:

`-2y=-5-7x`

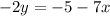
Dividing by -2 on both sides

`y=(5)/(2)+(7)/(2)x`

If we want to find one of the ordered pairs that are solutions we simply input a value for "x" in the equation, for example x = 0, and we would get the value for "y", like this:

`\begin{gathered} y=(5)/(2)+(7)/(2)(0) \\ y=(5)/(2) \end{gathered}`

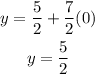
Therefore, an ordered pair that is solution to the equation would be (0,5/2). Like that, the other ordered pairs that are also solutions can be found.