Given the following series:
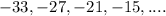
We will write the sigma notation for the given series
the given series is an arithmetic series becuase there is a common difference=6
we will find the explicit formula of the arithmetic series
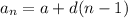
Substitute a = -33, d = 6
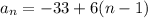
Simplify the expression:
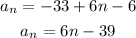
The sigma notation for the infinite series will be as follows:

So, the answer will be:
