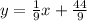Question

Bonus: Write the equation of a line in slope intercept form that isperpendicular to y=-9x+17 and contains the point (-8,4)*

Answer 1

First of all, to have two lines perpendiculars we need to remember that the multiplication of its slopes will be -1, we write this:

`\text{slope 1 }\cdot\text{ slope 2=-1}`

We deduce slope 1 from the given equation, comparing with a general form of the line, like this:

`\begin{gathered} y=mx+b;\text{ m = slope; b = intercept with y axis} \\ y\text{ = -9x+17; from this comparation we deduce} \\ \text{slope 1=-9} \end{gathered}`

Now we gonna find slope 2 throuht:

`\begin{gathered} \text{slope 1 }\cdot\text{ slope 2 =-1} \\ -9\cdot\text{slope}2=-1 \\ \text{slope 2 =}\frac{\text{-1}}{-9} \\ \text{slope 2=}(1)/(9) \end{gathered}`

finally, with that slope and the point (-8,4) we find a equation of a line, apply:

`\begin{gathered} (y-y_1)=m(x-x_1);\text{ m=slope 2; (x}_1,y_1)=(-8,4) \\ y-4=(1)/(9)(x-(-8)) \\ y-4=(1)/(9)(x+8) \\ y=(1)/(9)x+(8)/(9)+4 \\ y=(1)/(9)x+(44)/(9) \end{gathered}`

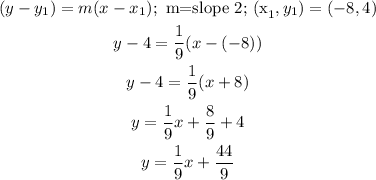
Finally, the equation for the line perpendicular to y=-9x+17 and contains the point (-8,4) is:

`y=(1)/(9)x+(44)/(9)`