The expression given is,
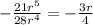
To prove if the left-hand side is equal to the right-hand side, we will reduce the left-hand side expression to its lowest term.
The left-hand side expression is,
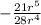
Factor the number 21 :
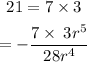
Factor the number 28:
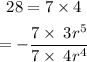
Cancel the common factor 7:
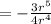
Simplify
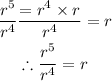
Therefore,
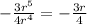
Now comparing both the right-hand side and the left-hand side, we can see that both are the same.
Hence, the answer is TRUE.