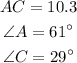Question

Solve the right triangle by finding all missing angles and sides.

Answer 1

Given:

There are given the right angle triangle, ABC.

Where,

`\begin{gathered} AB=5 \\ BC=9 \\ AC=? \end{gathered}`

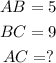
Step-by-step explanation:

To find the missing side in the given right angle triangle, we need to use the Pythagoras theorem:

So,

From the Pythagoras theorem in triangle ABC:

`AB^(^2)+BC^2=AC^2`

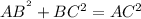
Then,

Put the all values into the above formula:

`\begin{gathered} AB^2+BC^2=AC^2 \\ 5^2+9^2=AC^2 \\ 25+81=AC^2 \\ 106=AC^2 \end{gathered}`

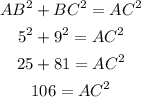
Then,

`\begin{gathered} AC^2=106 \\ AC=√(106) \\ AC=10.3 \end{gathered}`

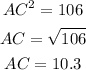
Therefore, the side AC is 10.3:

Now,

We need to find the missing angle in the given triangle ABC:

So,

To find the angle A, we need to use the formula of tan function:

So,

`\begin{gathered} tanA=(BC)/(AB) \\ tanA=(9)/(5) \\ tanA=1.8 \end{gathered}`

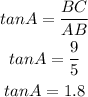
Then,

`\begin{gathered} tanA=1.8 \\ A=tan^(-1)(1.8) \\ A=60.9 \end{gathered}`

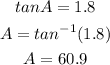
Now,

We need to find the value of angle C:

So,

To find the angle C, we need to use the angle of triangle rule:

So,

In a right-angled triangle, the addition of the two angles is equal to the 90 degrees.

Then,

`\angle A+\angle C=90^(\circ)`

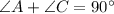
Then,

Put the value of angle A into the above formula;

So,

`\begin{gathered} \angle A+\angle C=90^(\circ) \\ 61^(\circ)+\angle C=90^(\circ) \\ \angle C=90^(\circ)-61^(\circ) \\ \angle C=29^(\circ) \end{gathered}`

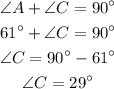
Final answer:

Hence, the missing side and the missing angles are shown below:

`\begin{gathered} AC=10.3 \\ \angle A=61^(\circ) \\ \angle C=29^(\circ) \end{gathered}`