Question

What is the average rate of change for this quadratic function for the interval from x=2 to x=4? A. -6B. 6C. 12 D. -12

Answer 1

We need to develop an equation for the quadratic graph.

We first look for the zeros (points where the graph cuts the horizontal axis) as they serve as the building blocks of our equation.

They are at x = -1 and x = 1

Thus, the equation is given by:

`\begin{gathered} (x+1)(x-1)=0 \\ x^2-1=0 \end{gathered}`

However, we have a negative graph so the leading coefficient is -1. This causes us to multiply all sides by -1.

`\begin{gathered} -1(x^2-1)=0_{} \\ -x^2+1=0\text{ is our equation} \end{gathered}`

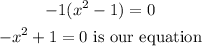
To get the rate of change, we substitute the relevant points and get their slope.

`\begin{gathered} Thus,y=-x^2+1\text{ is the function} \\ At\text{ x=2, we have} \\ y_1=-(2^2)+1=-4+1=-3 \\ At\text{ x=4, we have} \\ y_2=-(4^2)+1=-16+1=-15 \end{gathered}`

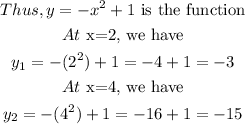
Next, we apply the all too famous gradient formulae:

`\begin{gathered} s=(y_2-y_1)/(x_2-x_1) \\ \text{where:} \\ x_1,y_1=(2,-3) \\ x_2,y_2=(4,-15) \\ s=(-15-(-3))/(4-2)=-(12)/(2)=-6 \end{gathered}`

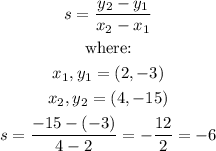
Therefore, the average rate of change is -6