Question

determine the open intervals on which the function is increasing and on which the function is decreasing

Answer 1

To determine the intervals at which the function is increasing or decreasing, we first need to calculate its derivative:

`\begin{gathered} f^(\prime)(x)=3\cdot3x^2+2\cdot9x-27 \\ f^(\prime)(x)=9x^2+18x-27 \end{gathered}`

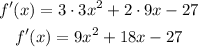
We need to find the values of the roots of the expression above:

`\begin{gathered} x=\frac{-18\pm\sqrt[]{18^2-4\cdot9\cdot(-27)}}{2\cdot9} \\ x=\frac{-18\pm\sqrt[]{1296}}{18} \\ x=(-18\pm36)/(18) \\ x_1=(-18+36)/(18)=(18)/(18)=1 \\ x_2=(-18-36)/(18)=(-54)/(18)=-3 \end{gathered}`

We can rewrite the expression for the derivative as:

`f^(\prime)(x)=9\cdot(x-1)\cdot(x+3)`

Therefore the derivative is positive when the signs of "x-1" and "x+3" are equal, therefore there are two possibilities, that they are both negative and both positive. We have:

`\begin{gathered} x-1>0 \\ x>1 \\ x-1<0 \\ x<1 \\ x+3>0 \\ x>-3 \\ x+3<0 \\ x<-3 \end{gathered}`

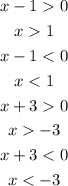
They are both negative when x<-3 and both positive when x>1.

So the function is increasing at the intervals:

`\begin{gathered} (-\alpha,-3) \\ (1,\alpha) \end{gathered}`

And decreasing on the interval:

`(-3,1)`