Question

Let g(x) = -2(3x + 4)(x - 1)(x – 3) be a polynomial function.Part A: Sketch a graph of the polynomial.Part B: Name all the horizontal and vertical intercepts of the graph Part C: State the end behavior of g

Answer 1

A.

In order to sketch this function, let's first find its zeros, by equating each term in the product with zero:

`\begin{gathered} -2\mleft(3x+4\mright)\mleft(x-1\mright)\mleft(x-3\mright)=0 \\ \begin{cases}3x+4=0\to x=-(4)/(3) \\ x-1=0\to x=1 \\ x-3=0\to x=3 \\ \end{cases} \end{gathered}`

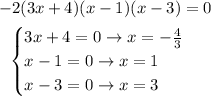
So the zeros are -4/3, 1 and 3. Since the coefficient of the higher order term is negative (multiplying -2, 3x, x, and x we have -6x^3), the function will decrease after the last zero and increase before the first zero.

Sketching the function, we have:

B.

The horizontal intercepts are the zeros of the function: -4/3, 1 and 3

The vertical intercept is the point where the graph intersects the y-axis, that is, when x = 0:

`\begin{gathered} g\mleft(0\mright)=-2\mleft(4\mright)\mleft(-1\mright)\mleft(-3\mright) \\ g(0)=-24 \end{gathered}`

So the vertical intersect is -24.

C.

The end behavior of g(x), since the coefficient of the higher order term is negative, is going to minus infinity.