Reflect over the x axis, then translate 2 units to the left
Step-by-step explanation:
To determine the transformationthat occured fromPQR to P'Q'R', we will use the coordinates of each letter and compare
P = (1, 1), Q = (2, 1) and R = (2, 3)
P' = (-1, -1), Q' = (0, -1) and R' = (0, -3)
We can see the y axis of P, Q, and R were negated to obtain the y axis of P', Q' and R.
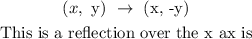
The translation that occurred on the x coordinates:
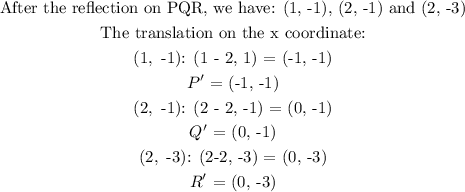
From the above, 2 units was subtracted from the x coordinate of PQR to obtain the x coordinate of P'Q'R'.
Subtraction indicate movement is to the left
After the reflection over the x axis, there is a translation of 2 units to the left