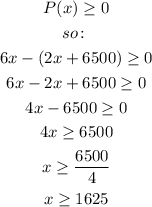Their revenue is given by:
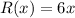
The cost by:
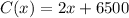
And the profit by:
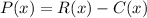
Since we need to find the profit when the company sellls 1000 pens, we need to evaluate the functions for x = 1000
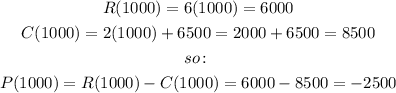
In order to find the number of pens needed to sell to break even. we can use the following inequality: