Given function is
![K(z)=\sqrt[]{16-z^2}](https://img.qammunity.org/2023/formulas/mathematics/college/tu6ppxooahg9p2vgd1bbr8s9komppko9ma.png)
Differentiating K(z) w.r.t z, we have,
![K^(\prime)(z)=-\frac{z}{\sqrt[]{16-z^2}}](https://img.qammunity.org/2023/formulas/mathematics/college/vhamchvgizylubfxuu600ai9qp24g5yrlp.png)
To find the stationary point, let us solve the equation K'(z)=0
![\begin{gathered} K^(\prime)(z)=0 \\ -\frac{z}{\sqrt[]{16-z^2}}=0 \\ z=0 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9p6do55ulhmxzsj7psydix0p98u3kugbha.png)
Now, we again differentiate K'(z) w.r.t z.
![K^(\doubleprime)(z)=-\frac{1}{\sqrt[]{16-z^2}}+\frac{z^2}{\sqrt[]{16-z^2}}](https://img.qammunity.org/2023/formulas/mathematics/college/363is8lig75f1ehk8v2txz535c9844jbbb.png)
At z=0,
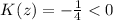
Therefore, at z=0, the function attains maximum value.
The maximum value of the function is
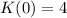
In the domain (-4,4), there is no absolute minima for the given function.