Question

Which cannot represent a proportional relationship select all that apply.

Answer 1

To represent a proportional relationship between y and x, the center of coodinates has to be part of the equation, as:

`y=k\cdot x`

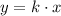
Graph A: Although the center of coordinates is not marked, we see that the line that fits all the points goes through the center of coordinates.

We can test that all the quotients y/x are constant, so the relation is proportional.

Graph B: the line has value y=5 for x=0. This is not possible for a proportional relationship, so this graph does not represent a proportional relationship.

Graph C: in this case, we see that y has a value of 0 for x=1. That is not possible for a proportional relationship. We can test 2 points and see that the quotient y/x is not constant.

This is not a proportional relationship.

Graph D: the line includes the center of coordinates, so it is a proportional relationship.

Answers: the ones that does not represent a proportional relationship are B and C.