ANSWER
• 5.38 lbs of the 64% alloy
,
• 46.62 lbs of the 35% alloy
Step-by-step explanation
Let x be the amount of the 64% alloy and y be the amount of the 35% alloy.
We know that the two amounts add up 52 pounds,
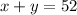
And that the 64% of x plus the 35% of y must be 38% of the third alloy that is 52 pounds,
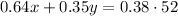
Solve the first equation for y,
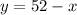
Replace into the second equation and solve the multiplication on the right side,
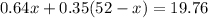
Distribute the 0.35 into the subtraction 52-x,
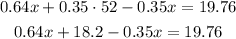
Add like terms,
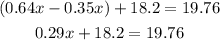
Subtract 18.2 from both sides of the equation,

Finally divide both sides by 0.29,
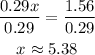
The metallurgist has to add 5.38 pounds of the 64% alloy.
To find the amount of the other alloy, we just have to replace x by 5.38 into the first equation where we solved for y before,
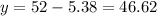
Hence, he has to add 46.62 pounds of the 35% alloy.