Question

(Note that most of the answers are algebraic expressions involving t) A car starts on a trip and travels at a speed of 55 mph. Two hours later, a second later starts on the same trip and travels at a speed of 65 mph. When the second car has been on the road trip for t hours, the first car has traveled 55(t + 2) miles and the second car has traveled 65t miles. At time t the distance between the first car and the second car is 110 - 10t miles The ratio of the distance the second car has traveled and the distance the first car has traveled is13t/(11(t + 2)). The second car catches up with the first car ____ hours after the departure of the first car.

Answer 1

The distance is given by

D = (Speed x Time) + Di

Car #1 has a speed of 55 mph and at time 2 hours its initial distance is 110 miles

Car #2 has a speed of 65 mph and at time 2 hours its initial distance is 0 m

We need to find the time when both cars will have the same position, then we have

`\begin{gathered} D_1=55(t+2)=55t+110 \\ D_2=65t \\ D_1=D_2 \end{gathered}`

So,

`\begin{gathered} 55t+110=65t \\ 110=65t-55t \\ 110=10t \\ t=(110)/(10) \\ t=11 \end{gathered}`

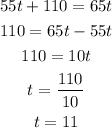
Therefore, the second car catches up with the first car 11 hours after the departure of the first car.