Question

I’m going to lose my mind if someone doesn’t FULLY ANDWER THE QUESTION STOP LEAVING THECSESSION AND ANSWER I PAY $35 A MPNTH FORBTHIS

Answer 1

we have the function

`f\mleft(x\mright)=xe^(\left(13x\right))`

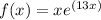
Find out the first derivative

`f^(\prime)\mleft(x\mright)=e^((13x))+13xe^((13x))`

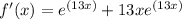
Find out the second derivative

`f^(\prime)^(\prime)\left(x\right)=26e^(\left(13x\right))+169xe^(\left(13x\right))`

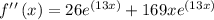
Equate the second derivative to zero, to find out the turning point or inflection point

`26e^(\left(13x\right))+169xe^(\left(13x\right))=0`

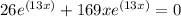
the turning point is (-2/13,0)

therefore

Concave up -----> (-2/13, infinite)

Concave down ----> (-infinite, -2/13)